Language Modeling Based on Neural networks: An overview

Introduction

Language modeling tries to capture the notion that some text is more likely than others. It does so by estimating the probability $P(s)$ of any text $s$.

Formally, assume we have a corpus, which is a set of sentence. We define $V$ to be the set of all words in the language. In practice, $\|V\|$ is very large, but we assume it’s a finite set. A Sentence in the language is a sequence of words

$$x_1x_2...x_n$$

where the integer $n$ is such that $n\geqslant1$, we have $x_i \in V$ for $i \in \{1 ... (n-1)\}$, and we assume that $x_n$ is a special symbol, STOP(we assume STOP is not a member of $V$). We will define $V^†$ to be the set of all sentences with the vocabulary $V$, $V†$ is a infinite set.

Definition: A language model consists of a finite set $V$, and a function $p(x_1,x_2,...x_n)$ such that:

1. For any $<x_1, x_2,...x_n> \in V^†$, $p(x_1, x_2,...x_n) \geqslant 0 \$
2. In addition, $\sum_{\substack{<x_1...x_n> \in V^†}} p(x_1,x_2,...x_n) = 1$, hence $p(x_1,x_2...x_n)$ is a probability distribution over sentences in $V^†$.

Methods

NGram Language Modeling

Here we will take a trigram language model as an example.

As in Markov models, we model each sentence as a sequence of n random variables, $X_1,X_2,...X_n$. The length n itself is a random variable. Under a second-order Markov model, the probability of any sentence $x_1...x_n$ is

$$P(X_1=x_1,X_2=x_2,...X_n=x_n)=\prod_{\substack{i=1}}^nP(X_i=x_i|X_{i-2}=x_{i-2},X_{i-1}=x_{i-1})$$

where we assume $x_0=x_{-1}=*$. For any $i$,

$$P(X_i=x_i|X_{i-2}=x_{i-2}, X_{i-1}=x_{i-1})=q(x_i|x_{i-2}, x_{i-1})$$

$q(x_i|x_{i-2}, x_{i-1})$ is the parameter of the model. Note, the parameter size of a $n$-gram language model grow exponentially as $O(V^n)$

Maximum-Likelihood Estimates

Define $c({u, v, w})$ to be the number of times that the trigram $(u,v,w)$ is seen in the training corpus.

$$q(w|u,v) = {\dfrac{c(u,v,w)}{c(u,v)}}$$

This estimate is very natural, but could run into a very serious issue. The number of parameters of our model is huge (e.g., with a vocabulary size of 10, 000, we have around $10^{12}$ parameters[I think there might be $10,000 * 10,000 * 10,000 = 10^9$]), many of our counts will be there, this lead to:

1. if the numerator $c(u,v,w)$ is 0, $p(w|u,v) = 0$. This will lead to many trigram probabilities being underestimated: it seems unreasonable to assign probability 0 to any trigram not seen in training data, given that the number of parameters of the model is typically very large in comparison to the number of words in the training corpus.

2. if the denominator $c(u,v)$ is 0, the estimate is not well defined.

There are some smoothing methods to alleviate these issues, but we won’t go there here, you could find out more details in the references.

The performance of ngram language model improves with keeping around higher ngrams counts and doing smoothing and so-called backoff (e.g. if 4-gram not found, try 3-gram, etc).

Language Modeling based on Neural Networks

Languae model based on ngram seems promising. It’s intuitively simple and we could always make it more representative by increasing $N$. However, the unique ngram counts go up exponentially as $N$ goes up, which means we need gigantic RAM to store those enormous amount of ngram counts. Neural network based methods have been exploited. The model size scales up with respect to vocabulary size(see section 2 of 10 for more details).

Feedforward Neural Network Language Modeling

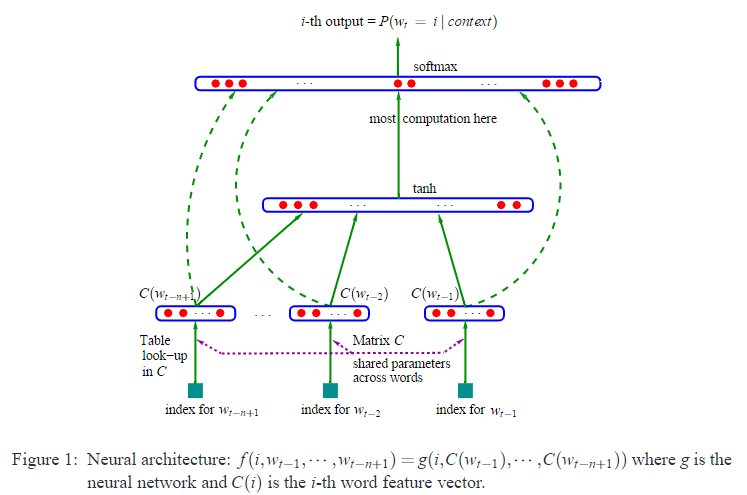
Architecture shown above models on the a slide window of the given sentence, which is $\tilde{P}(w_t|w_{t-1},...,W_{t-n+1})$ . RAM requirement scales with number words and window size.

The Forward passing is described as follows:

$$x=(C(wt−1);C(wt−2);...;C(wt−n+1)) \\ y = b +Wx + Utanh(d + Hx) \\ \tilde{P}(w_t|w_{t-1}, ..., W_{t-n+1}) = {\dfrac{e^{y_{w_t}}}{\sum_i{e^{y_i}}}}$$

Recurrent Neural Network Language Model

Figure 2: The Computational graph for Language model based on Recurrent Neural Networks.

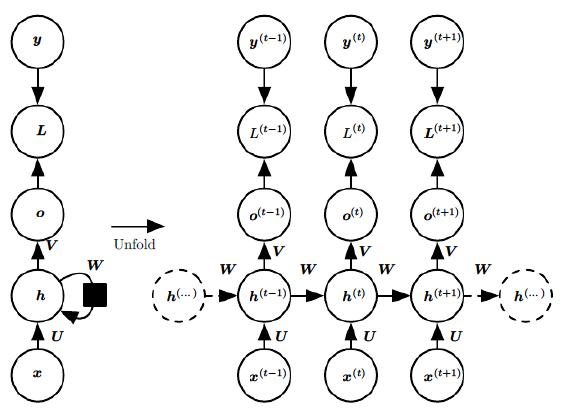
Forward Passing of rnn is described as follows:

$$a^{(t)} = b + Wh^{(t-1)} + Ux^{(t)} \\ h^{(t)} = tanh(a^{(t)}) \\ o^{(t)} = c + Vh^{(t)} \\ \tilde{y}^{(t)} = softmax(o^{(t)})$$

A major deficiency of the feedforward approach is that a feedforward network has to use fixed length context that needs to be specified ad hoc before training, it models on $P(w_t|w_{t-1},...w_{t-1})$. Usually this means that neural networks see only five to ten preceding words when predicting the next one. It is well known that humans can exploit longer context with great success. However, RNN encode the whole history into the state $h^{(t)}$, this makes it models on $P(w_t|w_{t-1},..,w_1)$.

Training Methods

Both feedforward neural network based language model and recurrent neural network based language model can be trained with back propagation with a cross entropy loss.

Evaluation Metrics

Perplexity

A common method to measure the quality of a language model is to evaluate the perplexity of the model on some held-out data.

Perplexity of a probability

The perplexity of a discrete probability distribution $p$ is defined as

$$2^{H(p)} = 2^{-\sum_{\substack{x}}{p(x)log_2q(x)}}$$

where $H(p)$ is the entropy of the distribution and x ranges over events.

Perplexity of a probability model

A model of an unknown probability distribution $p$, may be proposed based on a training sample that was drawn from $p$. Given a proposed probability model $q$, one may evaluate $q$ by asking how well it predicts a separate test sample $x_1, x_2, ..., x_N$ also drawn from $p$. The perplexity of the model $q$ is defined as

$$b^{H(p)} = b^{-\dfrac{1}{N}\sum_xlog_2q(x)}$$

where $b$ is commonly $2$. Better models $q$ of the unknown distribution $p$ will tend to assign higher probabilities $q(x_i)$ to the test events. Thus, they have lower perplexity: they are less surprised by the test sample.

The exponent above may be regarded as the average number of bits needed to represent a test event $x_i$ if one uses an optimal code based on $q$. Low-perplexity models do a better job of compressing the test sample, requiring few bits per test element on average because $q(x_i)$ tends to be high.

The exponent may also be regarded as a cross-entropy,

$$H({\tilde{p}}, q) = -\sum_{\substack{x}}{\tilde p(x)log_2q(x)}$$

where ${\tilde {p}}$ denotes the empirical distribution of the test sample (i.e., ${\tilde {p}}(x)=n/N$ if $x$ appeared $n$ times in the test sample of size $N$).

Perplexity of a language model

Using the definition of perplexity for a probability model, one might find, for example, that the average sentence $x_i$ in the test sample could be coded in $190$ bits (i.e., the test sentences had an average log-probability of $-190$). This would give an enormous model perplexity of $2^{190}$ per sentence. However, it is more common to normalize for sentence length and consider only the number of bits per word. Thus, if the test sample’s sentences comprised a total of $1,000$ words, and could be coded using a total of $0.19$(the wikipedia page says it’s $7.95$, I think it should be $190/1000$) bits per word, one could report a model perplexity of $2^{0.19} = 1.14$ per word. In other words, the model is as confused on test data as if it had to choose uniformly and independently among $247$ possibilities for each word.

Sample Sentences from language model using temperature sampling

Temperature sampling works by increasing the probability of the most likely words before sampling. The output probability $p_i$ of each word is transformed by the freezing function $f$ to:

$$\tilde p_i = f_\tau(p)_i = \frac{p{_i}{^{\frac{1}{\tau}}}}{\sum_jp{_j}{^{\frac{1}{\tau}}}}$$

For $\tau = 1$, the probability transformed by freezing function is the same as the output of the softmax. For $\tau \rightarrow 0$, the freezing function turns sampling into the argmax function, returning the most likely output word. For a low temperature $\tau \rightarrow 0^{+}$, the transformed probability of the word with the highest softmax probability tends to 1. For $\tau = 0.5$, the freezing function is equivalent to squaring the probability of each output word, and then renormalizing the sum of probabilities to $1$. The typical perspective I hear is that a temperature like $0.5$ is supposed to make the model more robust to errors while maintaining some diversity that you’d miss out on with a greedy argmax sampler. Maximum Likelihood Decoding with RNNs - the good, the bad, and the ugly digged more on the sampling process and he even proposes a generalized senmantic temperature sampling to solve semantic distortions introduced by classical temprature.

Reference

1. Bengio et al. Deep Learning, chapter 10 Sequence Modeling: Recurrent and Recursive Nets

2. Bengio et al. A Neural Probabilistic Language Model

3. Bengio Advances in optimizing recurrent networks

4. Mikolov et al. Recurrent neural network based language model

5. CS769 Spring 2010 Advanced Natural Language

6. Course notes for NLP by Michael Collins, Columbia University

7. Socher CS224d: Deep Learning for Natural Language Processing Lecture 8

8. Maximum Likelihood Decoding with RNNs - the good, the bad, and the ugly

9. Perplexity from Wikipedia

10. Bengio, Morin. Hierarchical Probabilistic Neural Network Language Model